These are my lecture notes of the 7. session of IE 602 System Dynamics Analysis and Design course in Industrial Engineering Graduate Program of Bogazici University. You can find the video of the lecture in Google Videos. The course is given by Prof. Yaman Barlas.
Links to the videos:
Part I
Part II (Turkish)
Part III (Turkish)
Interactive Gaming:
There is evidence that we human beings cannot make efficient decisions in complex feedback systems. By this we mean, we make a decision, we observe the results then we give another decision. These are feedback problems. In dynamic feedback decision problems, system has its life on own. System reacts to input and does all sorts of things as a result of feedbacks. You make a decision. system reacts. And you observe. Most feedback structures are nonlinear and delayed. When you combine them, we are not good decision makers. We under perform.
Controlled experiments may yield what kind of decisions decision makers ignore, overemphasize, utilize, have misperceptions, are there some generalizable inadequacies common to human decisions? These are decision making, cognitive questions. They are research questions we can research them in a controllable lab environment. This is phase 1.
Phase II is how can we excite learning in experiential environments. Is it possible to enhance learning in them? To what extent is it possible? Or is it possible at all You may think learning has occurred, but person only learned mechanics of the game. Here we men learning as understanding dynamic causalities, what structures play a role in this dynamic behavior of the system. That understanding we call learning.
We don't call learning, imitating some past successful actions. You don't understand dynamics of the causality structure. you may discover the mechanical tricks somehow. But you don't know why it works. You cannot transfer this knowledge to another problem setting.
By learning we mean understanding what goes on in the system.
Is that possible by game? That is interesting ques but not trivial. How can I separate learning from mechanical learning.
Finally we can make use of interactive games to cast some decision rules. Interactive games re nice platforms to test these rules.
You can use interactive gaming to test validity and robustness of models. Professionals in the field can test the model by using the games. That is a nice way of stress testing the model. These subjects can find uncovered structures.
Potential pitfalls in interactive gaming:
IG can be a fantastic tool if properly used. But it is very easy to misuse it.
1. People tend to forget that there is a model engine behind the screen. They can think that nicely designed user interfaces with a lot of informations are sufficient.
2. If you don't spend enough time to explain the problem setting, model and the game, their performance will be masked, negatively influenced by their ignorance of the actual problem in the model. Then they cannot further progress.
3. Preoccupation with technology. We are not in the commerce of games.
4. As a corollary of preoccupation with technology: Game mechanics become too complicated. Game should not be difficult to play.
5. Video game syndrome. The players aim to beat the game and get the highest score. Learning is not the aim.
Friday, March 23, 2007
IE 602 System Dynamics Lecture Notes 2007-01 - By Yaman Barlas
Posted by
Mert Nuhoglu
at
9:36 AM
3
comments
![]()
Labels: system-dynamics
Wednesday, March 21, 2007
System Dynamics Lecture Notes 2007-05
These are my lecture notes of the 5. session of IE 602 System Dynamics Analysis and Design course in Industrial Engineering Graduate Program of Bogazici University. You can find the video of the lecture in Google Videos. The course is given by Prof. Yaman Barlas.
Lecture Video Part I
Lecture Video Part II
Lecture Video Part III
Figures are here:
Tools for Sensitivity Analysis
1. Analytical sensitivity
2. By simulation experiment
One value at a time approach. You take each parameter in high low middle levels. Then leave it at middle. Do this with other parameters. If you have p parameters then you will do 3p experiments. The simplest approach.
3. Experiment design: Systematic way of carrying out experiment in simulations.
3.1
People say you need to change each parameter to each parameter level in all levels. This is full factorial design under experiment design. You have l^p runs. This assumes that there is no errors due to randomization. You have to experiment each data 3-4 repeatedly for stat estimation. Then it becomes an impossible problem. You use this in very small models. Or If you want to analyze only 5-6 parameters.
3.2. Fractional factorial design. Under certain assumptions you can get a good idea about the shape of response function of the experiment by not carrying out full factorial experiment but by fraction of it. Maybe by only 10%. It eliminates all... The simplest interaction term is two term inter. Higher terms very high number of experiment. If you have 10 variables, you can at most design two term or triple experiments. The design is called fractional factorial design. You make certain assumptions either high term inter don't exist. or they can be neglected. Or you know results that you obtain are tentative. Then you have a sample based on these assumptions. This is the starting point in your work.
3.4. Random sampling. Another reduction approach. Assume that full factorial experiment has hundred thousand required experiments. Then you take some random numbers and pick some of the experiments. This assumes you don't have any idea of the shape of the function. Because if you know the shape then you don't do totally random sampling. Now representativeness is important. It is rarely used.
3.5. Latin hypercube sampling. More advanced approach. Some sort of stratified sense. It is random but not purely. Each parameter rage is divided into N strata. That is they have N different values. For each parameter you randomly pick one value. One run is one random values for each parameter. Fig.5.1. You do this without replacement. You never want to try the same combination again. Next time you obtain another comb of parameter values. You repeat this N times. Number of values you tried. Full sensitivity of each parameter is focus. Focus is on if you have on parameter you have full detail of high resolution of this parameter. Since you do this without replacement, it assumes that all parameter effects are independent. This is quite restrictive. The adv is it provides with few experiments very homogeneous coverage of experiment space.
3.3. Taguchi design. Modern approach. Very practical design. It's a special quite reduced form of fractional factorial design.18 predefined tables are designed to fit most commons situations. A simple cookbook approach. Huge reduction of number of experiments. Assumption is most interactions are nonexistent. Few selected some two level interactions can be modeled. In all designs all higher order interactions are nonexistent. It assumes further parameter output relation is assumed linear.
Let's say the Output measure is amplitude. Fig.5.2. Question: How sensitivity is amplitude to ordering period. The assumption is Fig.5.3. This is not the model. This comes as a result of the solution of the model.
Fig.5.4. If inventory is equal to some K plus A time something. This is the solution of the model let's assume. A is amplitude of this oscillatory function. Taguchi design says A is a linear function of some parameter. Model can be nonlinear.
I think this is not a very safe assumption.
Q: Higher order inter are nonexistent, is assumed. Doesn't it contradict systemic approach. It tries to reveal inter effects.
A: In general this is true.We are building systemic models to discover simultaneous effects of multiples measures. But quantitatively changing values of parameters you cannot extract out the sensitivity of the output by increasing it values at different levels and by not simultaneous changing other levels. I am not sure the statements are equal. If model is linear, the two statements are equal.
Guidelines for sensitivity analysis:
We need to use our knowledge of the model to reduce number of experiment.
1. Seek behavior pattern sensitivity rather than numeric sensitivity. Don't spend months on numerical sensitivity of the amplitude in Fig.5.2. For example in Fig 5.4 seek the sensitivity that causes a to turn into b. From growing oscillation to damping oscillation.
2. Positive feedback loops have in general more influence such strong behavior pattern sensitivity of the model. They are destabilizing loops. They are crash or growth lops.
3. Range of parameter values that you try out. When you do sensitivity analysis especially for parameter estimation and policy analysis. Restrict parameter set to a realistic set of parameters. But you can do this for validity testing.
4. You may have some parameters estimated using stat tools. On these parameters you don't need extensive sensitivity testing if they are not decision parameters.
5. When multiple parameters are simultaneous altered, you know that in real life it is inconsistent that death rate is much higher and birth rate is much lower. When death rate goes up birth rate goes also up.Not for validity testing.
Mathematical equations:
To show you idea of feedback sensitivity.
Mathematical Sensitivity Analysis
Definition: Sensitivity of S^M_K M:output measure, K:parameter.
Equation 5.5
If you find M=f(k) you need have derived the solution. You can not find solution in general in dynamical systems.
e.g.. A linear (feedback) dynamical system. In block notation: Fig.5.6.
What transfer function does is it multiplies r and obtains C.
G: Transfer function in frequency (s) domain. Then C=r G. Here C would be in s. First you take Laplace trans to obtain G.
This Fig.5.6 called open system.
Sensitivity of output C wrt G. S_G^C. Equation 5.7
This is clear because of C=rG.
Now consider adding a feedback loop.
Fig.5.8
You observe output and do something. These inputs and outputs are not flows. G is not derivative of flows. This has integrations in itself, but it is block diagram and just means C=rG.
When you have two lines entering into a block, you take plus and minus, that is the difference. e.g. you take an action based on difference of desired inventory and measured inventory.
Mathematically 5.9 C=(r-b)G
b=cH
C=(r-cH)G...
So combined block is 5.9.a
5.10
This is 5.10.a is sensitivity of percent change in C to G. The higher H, the lower sensitivity, in general. It is not anymore a constant sensitivity like 5.7.a.
Reduced sensitivity of negative feedback control system.
Posted by
Mert Nuhoglu
at
10:48 PM
0
comments
![]()
Labels: system-dynamics
Tuesday, March 20, 2007
IE 602 System Dynamics Lecture Notes 2007-04 - By Yaman Barlas
6 March 2007
Sensitivity Analysis:
You have a model fully validated. You are satisfied. Next, you are going to use as an experimental lab to carry out analysis and design improved policies.
Figures are here:
So broadly speaking what is analysis and design?
Analysis means understanding something. Studying something to understand it. IN our context means understanding why and how. By what causal mechanisms and which ways the model behave as it does. Understanding sources of dynamic behavior. This is prerequisite to redesign it. Here main comps of analysis"
One extreme form of analysis is mathematical solution. Dynamical model, if you can solve it, you obtain an equation which is an explicit function of time. The solution is a vector variable =s which are explicit functions of time. Sines, cosines, exponentials can be complicated. But in any case these are time functions. And various parameters of functions freq, exponents come from model. You can quiet precisely say what parameter does what?
Simple birth death population. Solution of a linear pop model is p(t) = p(0) + ... If b = d, you have const pop. The larger difference, larger slopes you obtain. This is an extreme form of precision in math analysis.
This is only true for linear systems. For almost all linear systems, you can obtain math solutions. And for almost all nonlinear systems you can’t obtain a mathematical solution. Well come back to this in what conditions are mathematical solutions possible?
Next level is equilibrium solutions and analysis. We'll talk about this a lot. System stays at these equation points.
Third comp is sensitivity analysis. This is major subfield of analysis. To what extend in what ways (qualitative and quantitative questions) do behavior changes to the changes in initial conditions and structure. This percentage change in dynamic behavior patterns is a major field of analysis.
Policy analysis: Given that you have a certain policy how sensitive is this policy to the parameters, initial conditions of the model. Specific application of sensitivity analysis to policy.
Then there is design. Obtaining improved policy: How can I obtain policy structure that will yield and improvement in system behavior? A dampening of pop growth, stooping cancer growth as a result of medical intervention, higher percentage of students entering in universities as a result of university placement policy.
The limit of design is optimization. Given my objectives this is the best possible policy. This is rarely possible in nonlinear feedback models. There are no easy algorithms. This is a great research area.
Now our topic is sensitivity analysis and policy analysis experimentally.
Different uses of sensitivity analysis:
· Model validity testing
· Evaluating importance of parameters: Value of information and importance of parameters. If behavior is sensitivity to a few parameters but insensitive to some other parameters. Then these parameters are import.
· Decide on which parameters you need to spend more effort. These are most sensitivity parameters. Then you know that 10% error in these parameters are import. You need to estimate them better.
· Understand the structure behavior connection. This is mathematical analysis. Mathematical solution constructs time function of behavior in parameters of model. You see the direct links. We can't do this mathematically so let's try to do it with sensitivity analysis. We make series of simulation runs. And decide the role of each parameter. Model behavior connection can be established by doing sensitivity analysis to some extent.
· Evaluating policy alternatives. Sensitivity analysis is applied to some policy. How sensitive is our policy to some set of parameters? If it is very sensitive you don't like it.
High sensitivity may mean:
· weakness in model
· discovery of critical parameters
· need for further research to estimate parameters
· most important parameters for behavior
· weak policies
Types of sensitivity analysis:
This is important.
Sensitivity with respect to:
· parameter (or initial) values - i.e. numeric values.
· numerical - a model with behavior like Fig. 4.7. I make some parameter changes. I obtain b). This is numeric change. It is trivial change. Mathematically there will be some numeric sensitivity with any change of the parameter. The question is how much. Whether it exists or not, is not important.
· behavior patterns - This is very different Fig.4.8. b) has a very different type of change. This is oscillation but it is damping. A change from a to b is pattern sensitivity. Can you guess which is more important? Behavior pattern sensitivity is more important than numeric sensitivity.
Next question is: Do you expect behavior change to come from what? From structure changes. Feedback structures that have enough loops, that is control loops, organizations that exist and survive, as a result of negative control loops. These interesting problems have enough negative feedback loops that cause them persist so many years. Even
Alternative structures - you change the structure. You write a new equation. You remove a feedback lop. You modify the structure.
Somewhere between there is form of functions. This may be closer to parameter change or structure change. Fig. 4.5 You modify the level of function. This is parameter change. On the other hand, if you change the form of function, Fig. 4.6., this is more like a structure change. And another change is c). It removes the relation between y and x.
Some observations:
Fundamental behavior is created by some dominant feedback loops. We'll talk about this.
Discovery of sensitivity parameters are critical. And of course discovery of structure mostly influential in creating fundamental behavior is important.
S: What if birth rate > death rate or death rate < birth rate in population growth model? This changes the behavior pattern...
When you choose 0 parameter value, you are saying that it doesn't exist at all. This is clear structure change. In your case, a change in parameter value causes a significant behavior change. But this is not structure change. Same structure.
Tools for sensitivity analysis:
They are either analytical: What percentage of change in output is caused by what percentage of parameter? For linear systems you can obtain it.
Much more extensive is simulation based experimental sensitivity analysis. How do you do it? Experimental design.
Experimental design is scientific way of organizing experiments.
Posted by
Mert Nuhoglu
at
10:32 PM
0
comments
![]()
Labels: system-dynamics
Sunday, March 11, 2007
IE 602 System Dynamics Lecture Notes 2007-03 - By Yaman Barlas
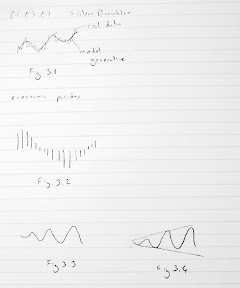
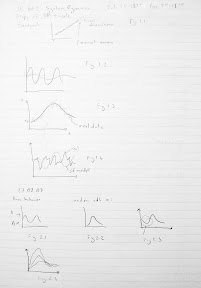
01 March 2007 20070301 BTS (Behavior Testing Software) Tools in BTS Slayt grafikler Assume that a certain system has these types of behavior. Fig.3.1 First graph (model generative) has near perfect fit. Second: error: trend. Since there is a trend error, means differ. Thus ac function can’t be found. Third: period error. Can you discuss phase angles? They will be periodically in or out of phase. Fourth: First has almost non-modellable noise. Fourth noise is questionable. Modellable smaller period noise. Autocorrelation function or spectral density function will reveal this smaller oscillation. Variance of real data will be larger. Fifth: out of phase. Cross correlation function will give a maximum at a certain lag. It can give a lag error but it will be random like 1. Sixth: mean error Seventh: amplitude error First you need detrend the data. Then do smoothing. Then check the periods. Until you remove period error. Then check phases and so on. So there is a logical order of tests. Trend removal: Models can be linear, quadratic, and exponential. Take cross products and take the average. That is covariance function. Then there is notion of lag. If there is no lag, then it is covariance. If no lag, covariances in the data that are one lag apart. k can be at most 1/5 of the data. Covariance is a number it can be positive or negative. If large then there is a large covariance negative or pos. But how large is large? You normalize it. To normalize it, you divide it by max possible covariance. Max possible covariance is at zero, this is actually variance. This is famous autocorrelation function. By definition it is less than one. Any value which is statistically significantly larger than zero means, there is a significant covariance at lag k. One specific usage is to estimate the period of data. You can also prove that, if periodicity is t, autocorrelation function has period of t. That way time series is very noisy, autocorrelation function will be noise free. Another useful usage: general comparison of autocorrelation structures between real data and model generated data. AC is signature of data. AC is hard to.. Higher order sophisticated smaller movements in real data are captured by model itself? Ac structure of data and ac function of model. This is signature. Rather than comparing g real data and model generated output one by one. If you do that, you get huge errors. Then compare their signatures i.e. autocorrelation functions. Do the ac functions differ at any lag significantly? Each ac function is a statistic. Using variance of ac function, you construct confidence band or control limits. H0: All r (variance sanirim) are equal. At all lags. It is all multi ... test. It is hard to estimate alpha value of function, because it is not a single test. If you reject, only one is ejected. It is hard problem. They are not independent. If you reject at lag 2, you may also reject at lag 3. They are not independent hypothesis, they are auto correlated too. Alphas are not clear, but test is okay. Estimating spectral density function: It is Fourier transformation of ac function. It is a function of time. That is it is in time domain. You transform it to obtain a function in frequency domain. S is frequency. SD function details won't be discussed. You transform ac. Then use windowing (filtering) technique. Then you can estimate power. It can amplify dominating frequency. Then show you more than one frequency. Next tool: cross correlation function. You take inventory data. Definition is very similar to covariance. You compute cross covariance. ... If you divide ... that is Pearson. Can I come up with computer their correlations at any lag? This is then, cc functions S and A. It is symmetrical around zero. Fig.3.2 is a cc function. There is reasonably large ac at lag 0. Then they are in phase. So cc finds the delays between model and real data. Another usage is you compute cc between inventory and production variables in the model and cc shows a phase lag. Then you compute cc between real inventories and real production. Then are the phase lags consistent? To compare the means you use t test etc. Next problem: comparing amplitudes. You need curve fitting. First approach: fitting trigonometric functions. You fit trigonometric function to real data and model data. Once you fit, trigonometric function gives you amplitude. Then you compare A's (amplitude). This is the easiest way. You have to linearize trigonometric functions. Second approach is Winter's method of forecasting. Winters method is designed to forecast seasonal data. These are not seasonal. Seasonal means oscillatory. attributed to auxiliary var. Oscillatory is not have to be attributed to auxiliary var. SD says these oscillations don't need to have exogenous causes. These are endogenous generated oscillations. Winter's model: X=(a+bt)*F+e F is a max at peak season. bottom at low season. Then there is base value. Forget b. there is no trend. Question is you have to estimate F for different time points. The notion of season is different, it is where you are in the cycle. How do you estimate amp? F values difference between max and min. Then unnormalize them. Third app for amp estimation: simple trigonometric fitting fails because of too noisy amplitudes or somewhat noisy periods. So single sine wave is problematic. you take portions of data. Then you estimate different amps. Then average them. Next tool: Trends in amp. You fit a sine wave. Then you compute a succession of sine waves. Fig.3.3. Then you fit a regression line to these estimates of amps. Then you get something like Fig.3.4. Last: People preoccupied with single measure. Audience asks you give me r square. That is the habit of regression. If you say 0.95 that is great. In SD you resist this. We know that single measure of validity does not exist. A research project of a single summary of discrepancies in models. You some sort of normalize all measures. As of today this doesn't exist. Since there is so much pressure. We use some measure better than r square but not quite valid for system dynamics: discrepancy coefficient. Comes from Tails inequality coefficient. It is a normalized measure of error between real data and model generated output. What it is, is, error between S and A (both normalized) divided by their own natural variances. This is equal to s_E std dev of errors divided by s_A (std dev. of real data) + s_S (std dev. of mdodel data) Smaller it is, better. How large is large is unclear. A highly valid model can create 30% coefficient values. More important is decomposition of U (coefficient value). Any value of U is not that imp. Three decompositions of U exist. U1+U2+U3. These are additive. Percentage decompositions of U. from means (U1), variance(U2) imperfect correlation (U3). If U3=0.97 error comes from imperfect correlation. This is acceptable, because perfect correlation is not possible. This decomposition is more important than value itself. Beyond high U3 is unnecessary fine tuning. End of validity discussion. Presentations and papers in moodle.
Posted by
Mert Nuhoglu
at
8:00 PM
0
comments
![]()
Labels: system-dynamics, validity
IE 602 System Dynamics Lecture Notes 2007-02 - By Yaman Barlas
26 February 2007 Structure Validity - Verification Differences Methodology to indirect structure testing software: In general, you can't examine the output and deduce the structure from the behavior. This is general fact. But logically, write the expected behavior under extreme conditions. Mantıksal tahminlerle, aşırı durumlarda, sonuçtan çıkarak yapıyı tahmin edebilirsin. There is first of all a base behavior. Fig. 2.1 In condition c, we expect some other behavior pattern, which is different than base behavior. Fig.2.2 But there is a subjective part as well. If the behavior is a little different like Fig.2.3 is this acceptable? SIS Software: 1. Teach the template of dynamical patterns. Program should recognize the patterns. E.g. Decline: subclasses: can go to zero or not Growth and decline: subclasses: not S shaped growth, but a goal seeking growth. There are about twenty patterns to categorize all the fundamental patterns. Pattern recognition: Complicated pattern recognition algorithms are about faces, handwriting. But they are not fit for functions. They don't exploit the properties of functions. Any function is a succession of curves. With two derivatives and ranges on these, we can summarize dynamical pattern of slopes and curvatures. For example, a curve might have such ranges: In the first range first derivative is positive, second is negative, then an inflection point. And so on. States are characterized by these two components (first derivative and second derivative). Then you can characterize both derivatives being negative, second zero, first positive so forth. So a pattern like Fig.2.2 can be summarized by a few successions of states. We have some more measures: Constants: are they zero or more? Then you give hundreds of noisy data of each class. E.g. for Fig.2.2 the bunch in Fig. 2.4 are training data. They all belong to overshoot and decay to zero class. Computer brings some sort of probability matrix of the state transitions. Then it produces transition probability matrix. Then it saves them. So, it averages all these. Then stamps class transition probability matrix. This is sort of signature of this class. You give some noise for patterns, for example you can add one more transient growth before the expected decay. It should probabilistically distinguish the data that looks like some pattern and determine to which class the data is closest? The likelihood to belonging to a class is maximized for one of the classes. Fig. 2.5 The algorithm is explained in thesis or working paper. Example just to prove it works. Base behavior of a model: Change the parameters and obtain n output. Fig. 2.6 what is the new pattern? Algorithm says new pattern: negative exponential growth. Parameter Calibration Fig.2.7 For example, the aim is to change the growth to an s-shaped growth from exponential growth. Is this possible? Gönenç bu konuda çalışıyor. It runs all the combinations of parameters. But these combinatorial run becomes too many. Then it says best parameters. Bu araştırma konusu çok yüksek getiri sağlıyor. Bu arama işlemi, akılılaştırılabilir mi (intelligence)? Gönenç çalışıyor. Heat algorithm, genetic algorithms heal climbing. They depend on problem instances. Eğer çok sayıda yapıda çalışan algoritma bulabilirsek, bu araştırma olur. Tek bir yapıda değil. Modellerin benzerliğinden kasıt: modelin yapısı. Bu aslında matematiksel fonksiyonun biçmidir. Calibration with input data: SIS: Bu konuda ödevler verilecek. Behavior Validity It focuses on patterns, but not like pattern classification problem. It is qualitative. BV is quantitative validation. Real system is oscillations class, is my model behavior oscillatory? This is not the subject of behavior validity. Fundamental behavior is oscillatory. Then compare the patterns. What are pattern components of oscillations? Fig.2.8. Trend, period, amplitude. More measures? Phase angle? That is how it starts? Önce inişe mi geçiyor, çıkışa mı? For many patterns it is like Fig. 2.9 (overshoot and decay). What components? Max, equilibrium, time points, slopes Dynamics of any system can be stated in two parts: transient, steady states. Fig.2.10a. Any dynamical system has these. Transient is caused by initial disequilibrium of system. After initial disequilibrium goes away, what the system does is steady state. This has no dynamics in Fig.2.10a. Whereas in b steady state behavior is damping oscillation. There is a big difference between two. You can apply this to every pattern. You can even have very strange dynamics like in Fig. 2.11. In steady state, there is a succession of boom and bust. Then equilibrium, then again boom and bust happens. Steady state is a succession of overshoot and equilibrium. Fundamental difference between these two: a) There is a steady state and transient state b) There is only transient Statistical estimation cannot be applied to transient behavior. There is no repeated data thus you can’t obtain x bar i.e. average. You have to have repeated date. You can statistically compute the period of 2.10b. In Fig. 2.11You can statistically compute period but not maximum. In 2.10a, there is a single pint. For that reason transient behavior is not analyzed by statistical estimators. This is life cycle problem. A business collapses. Another example is some goal seeking control problem, thermostat. It just arrives to a constant temperature. They don’t have repetitive data. Behavior Validity Testing Software: BTS II First question: is it transient dynamics? Then you forget statistical estimations. You just find graphical measurements: maxima, minima, inflection points, and distances. In steady state there are more statistical measures: like trend regression, smoothing. First thing, to do: detrend (remove trend) the data. If any time pattern has trend in it, most of statistical measure, like variance, mean, autocorrelation functions are impossible to estimate. Most stat measures are related to x bar. If x bar doesn't exist, then you don have them. Is there a trend? If there is, estimate trend and remove trend. (Trend regression) Then you do smoothing. This is for real data. In model, you turn off noisy parameters. Fig.2.12. It looks like oscillatory behavior. First smooth this by filtering like moving averages, exponential smoothing. Rest is standard tools. Multi-step procedure: Barlas has ready packages for statistical measures. Otomatik olarak islemleri yapiyor. Autocorrelation: Estimate autocorrelation function, they are like signatures of dynamical patterns. How successive data points are related. 0: 1. How 1 is correlated to 0 point. Fascinating is it doesn’t only show short term autocorrelation of model. Kısa dönemli korelasyonla, uzun dönemli korelasyon farklı. AC data has periodic behavior. At 22 is the peak again. That is not coincidence. This 22 is the estimate of noisy oscillatory time series. If time series is periodic, autocorrelation is periodic with the same period. Take difference between two autocorrelation functions. Find 95% confidence band. Difference lies out of the band. Then you reject the hypothesis. Spectral density function is transformation of ac function in frequency domain. Fourier transformations of ac function in s domain. Spectral density function use windowing technique. To exaggerate peaks. It is stat estimation technique. This ay spectral density function will show peaks frequencies at which time series has max energy content. It is also called power spectrum. Power content of time series is maximal at what time points? This will peak at dominating frequencies. Max occurs again at 20. Cross correlation: It is a measure that (ac was how in a given time series successions. time points are correlated?) cc is good old correlation function. How x and y are correlated? Take two data sets as x and y. You cross multiply x and y. Then divide by standard dev. That is Pearson correlation function. If it is positive, then data are positively correlated like lung cancer and cigarette smoking. CC is a generalization of that. I give you x and y. Cross correlate by different lengths x1 time y2. CC is a function of lag; only at lag 0 is good old correlation. Function is to find at any lag the cc of x and y. (Slayt PPde) If at 0 the peak: then they are at perfect phase. When out of phase, peak somewhere else. Amplitude: Compare discrepancy coefficient. Single measure that summarizes overall numeric fit. Next time I will show formulas. Compare trend in amplitude:
Figures are here:
Posted by
Mert Nuhoglu
at
7:55 PM
![]()
Labels: system-dynamics, validity
IE 602 System Dynamics Lecture Notes 2007-01 - By Yaman Barlas
Methodology
Model validity testing starts when you smart modeling effort and it is distributed through all phases.
This lecture is about model validity testing.
Conceptual and Philosophical Foundations
Most of these are from IE 550.
Major distinction between statistical models and system dynamics models (theory like models, transparent). System dynamics models claim to explain the causal description of real processes.
Fundamental difference: short-term forecasting model is valid if it provides accurate enough short-term forecast.
Validity is measured by accurate enough forecast.
Fig1.1
After observing real points you update your forecast model. So each time you obtain a few points ahead. Then see the error and update the model. This is called as: ex-post prediction. Ex-post means after having observed new information.
These models don't claim any causality.
E.g. it is demand for automobile tires. It may depend on mile consumption, bankruptcy, some function of time.
In system dynamics there are different aspects of validity.
1. Behavior validity. Similar to statistical validity. But this is only one component.
2. Structural validity. This has greater importance. Causal justifiability of the model. Do the relations in the model reasonably approximate the real relations in the problem? System dynamics problem is valid, a) it has acceptable structure and acceptable representation of the real structure b) it can reproduce the dynamical behavior patterns of the real world.
Motto is:
The right behaviors for the right reasons.
This means, both behavior and reasons are important for validity.
System dynamics models are in the domain of science.
It is not only statistical problem. You are trying to convince the people for the structure. It is a simplification of the reality but it is a good simplification. This is like a good cartoon. Charlie Chaplin, Alfred Hitchcock, a few drawings: there is a cigar, fat man. If you know Hitchcock, you know immediately that it is a good representation of him, although it has only 5 lines of him. I can draw him with 25 lines but it won't be good. All great cartoon drawers have this ability. With only a few strokes they are able to represent the real person.
Models are like that. They are extreme simplifications of reality. This act in arts, we can not proceed in science in this way very easily. E=mc2 you can not look and see yes this is correct.
How do you convince people? This simplification is a good representation that it is a good representation of real world. This is a whole philosophical debate.
There is a discussion, can we positively prove, that a scientific theory is valid representation of reality. Some logical, positivists argued that this should be possible. Relativists argue that there is no absolute truth. All models are temporarily acceptable. These are all conventions. We can never prove that the model is valid representation of the reality, even if it can be a simple event. You try to establish confidence. Science is an act of confidence in building validity of models or theory.
System dynamics: validity testing is establishing confidence in the credibility of the models. There is no true, wrong model. Sterman: "all models are wrong". That is true philosophically. The question is which ones do you still use? Structural validity indicates a spectrum, not of yes or no. you have models that are great, fairly valid, so so, bad....
By the way, I talked about statistical significance is also a problematic term in philosophy. For one reason is, test of hypothesis is: H0: model is reality. Can we assume the equality? Alternative hypothesis is it is not equal. If you reject h0 it is a strong result, useful result. H0 assumes a state of world. H1 rejects it. If you cannot reject, there is a weak result, you cannot say anything about the outcome. You rejected h1 but you don't know the why the outcome came out. This is the foundation of statistical hypothesis testing.
H0 says: model statistically equals real world. If you reject h1 it is not practical. If you didn't reject, you don't have anything strong.
In policy analysis is strong. Model behavior is real behavior. h1: amplitude is
By rejecting in policy analysis H1, you obtain a strong result.
Why is structural validity so important in system dynamics? Practical reason: these models are built to understand how problems are generated, and come up with new policies to improve the behavior of system. Without structural validity how can you play with structure to improve policy behavior? Structural validity is essential in system dynamics, because the problem is not forecasting. I claim that new policy, inventories will be improved. Fig 1.2
Point predictive ability is behavior validity. In system dynamics, point forecasting nearly impossible, should not be expected from a system dynamics model. Point forecasting means point by point measure of errors. Ex-ante term: system dynamics models provide ex-ante predictions. You don't do curve fitting.
In statistical model this equation is a model. In system dynamics the curve doesn't even exist. It is outcome of the model. There is a big difference. Everything is done at time 0. The laws are given and you let it go. fig.1.3
In comparison, system dynamics has very successful output validity. Real data may very well. Real data may be far more different than statistical model. In fluctuating patterns, real data can be much further. You have noise in real systems and they are auto correlated in real life. Fig 1.4 you can easily get huge errors although you can represent the oscillating pattern.
System dynamics models provide pattern forecast rather than point forecast. this model says following: I am forecasting with a given set of relations, given set of initial conditions, the behavior of pattern will be damping oscillations, or collapse followed by growth oscillations. This is a forecast about behavior pattern. This distinction is terribly important. You are predicting but never will we compete with other models, even verbal models in the power of point forecasting because ex-ante models are not suitable for this. This is also true for chemical or scientific models.
Ex-ante: very weak point predictors but strong for behavior prediction.
Overall Nature and Selected Tests of Formal Model Validation
Again you know from IE 550.
Outline:
Validity testing:
· first structure validity (big)
· then behavior validity (smaller)
Structure validity
· as you build you make direct tests:
· structure-confirmation
· parameter-confirmation
· direct extreme condition
· dimensional consistency
· Indirect structure tests: (whole model) structure oriented. Whole system in connections. Does the whole have coherence?
· You do simulation runs, and by observing runs, can you say something about validity of the model.
· In theory you cannot: in automata theory: a given output can be generated by an infinite number of structures. So by looking at output you cannot deduce structure.
· Thus we do special simulations: extreme condition, phase relationship test...
· Most important: extreme condition test. If you run model under some specifically chosen extreme conditions, prior running the model, you can logically deduce what the result will be like. E.g. population model. Let us run with 0 woman population. You know the population will decay to zero. You know also the pattern of behavior.
· Question: is extreme condition so important, if there is a better operating model under normal conditions.
· Response: if the model yields a behavior pattern under extreme conditions. several possibilities exist:
· Model discovered something weak point in your problem.
· Model does not cover certain ranges of model. You spend your effort in other areas of model. You consciously know that. That is okay. But you have to face it.
· Model teaches you something. You have such a good model. When you run it, you obtain a pattern you were not expecting. You learn something that you didn't realize. That is the greatest benefit.
· How do you do these indirect tests?
· Sis software: indirect structure testing software. It does try to automate these dynamical patterns, you can write down the expected outputs. Then the software will make all these runs to categorize the outputs obtained. It recognizes the patterns. There is an attempt to automate the process.
· The problem in these indirect tests, you end up with 1000s of simulations and horrendous task to visually check each output.
· behavior sensitivity:
· Boundary adequacy: two versions: 1. you add a new structure to the model. There is a questionable variable. You run the model with new structure if the model doesn't add a new pattern, the new structure is not necessary. 2. You remove some structure that looks unnecessary.
· Phase relationship: important. You don't compare sales to sales in real data. You compare e.g. phase relationships between finished inventory and raw material in the model and reality. This will tell you about weaknesses about delays involved.
Behavior validity: more statistical. Remember this is about: I know I have a valid structure. Can I establish dynamical behavior pattern of real system by the model. Are they closed enough. Are the patterns closed enough, not the patterns? Then you have to define patterns firstly. Patterns might be trends, oscillations, amplitude, period, slope of damping envelope, curvature of the overshoot and decay, max-min points.
1. Define patterns
2. Measure them
3. Compare patterns of reality and model
· We have software for this: BTS.
Posted by
Mert Nuhoglu
at
7:40 PM
0
comments
![]()
Labels: system-dynamics, validity